If you have young kids like I do, you probably know all about Stikeez. If not, you are probably wondering what the fuss is about.

Pick n Pay’s latest promotion has caused quite a stir as far as I can tell, filling the airwaves and social media with equal measures of delight and disgust. It brought the whole collection craze thing to the fore again after years of relative calm.

Store posters implore you to “collect them all”, and some folks are desperately attempting just that before the promotion ends on 20 September. Let’s look at how challenging this will be.

Obviously you need to collect at least 24 Stikeez to have a complete set of 24. At the rate of R150 per Stikee this necessitates spending at least 24 × R150 = R3 600 at Pick n Pay over the course of 7 weeks (ignoring bonus Stikeez). This is a lower limit, though, since you receive random Stikeez at the till and will soon have duplicates. Just how much more than 24 do you need?

For starters, the chances of getting a complete set after collecting the minimum of 24 Stikeez are extremely slim: one in 2 149 632 061 to be exact. You will have way better luck winning the Lotto at a meagre one in 13 983 816, so let’s forget about that option.

Mathematically speaking, collecting Stikeez is an instance of the coupon collector’s problem. While doing the math can be fun too, I found it more rewarding to simply simulate this process on a computer.

If you assume that Pick n Pay ordered equal amounts of each Stikee (see Part 3 for more on this) and that the Stikeez bins at each till are completely randomised, you get the following approximate distribution for the number of Stikeez you need to collect:

It does not look good.

The median number is 85, which means that even if you collect 85 Stikeez you will only have a 50/50 chance of completing your set. To be 90% sure that you get your set, you have to pick up 128 Stikeez.

Let’s put that in Rands. If you spend 85 × R150 = R12 750 at Pick n Pay, you have a 50% chance at success. If you splurge 128 × R150 = R19 200, you still only have a 90% chance. And you only have 7 weeks, making this a very unnatural shopping experience. Of course, you could be one of the unlucky few for whom even that amount of money is not enough…

If you need more than one set, say one per child, things are even more dire. The median number of Stikeez is 130 (R19 500) for 2 complete sets and 169 (R25 350) for 3 sets.

Why is it so bad? The inherent nature of collection through random draws is that there is a lot of euphoria at the start when the unique thingies keep rolling in—and then it all dries up and despair sets in. The very last Stikee you need has a probability of 1/24 of showing up, which is about the same as you correctly guessing which letter I’m thinking of, and the letter changes after every guess!

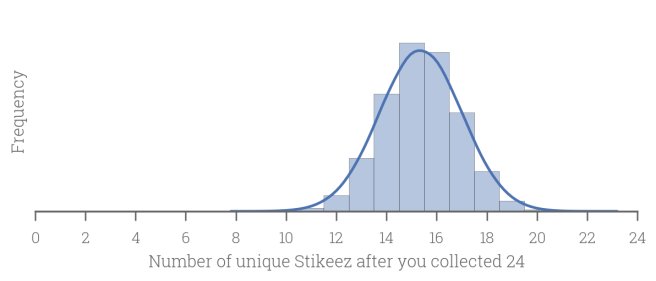
Here is another graph to highlight this effect. It shows the approximate distribution of unique Stikeez after you collected the minimum amount of 24, hoping in vain that you would have a complete set:

While you did not make it (fat chance!), you still have about 14–17 unique critters. You are already about two thirds of the way, so you probably only need about 12 more Stikeez to get there, right? Notice the lack of despair…

My own collection pictured above bears out the statistics. I have 15 unique Stikeez in a sample of 25, so that’s pretty average going.

How do you get that elusive complete set? You have to be either very wealthy or willing to beg at Pick n Pay entrances for the mercy of the childless and disinclined, it seems.

Or you could read Part 2, which examines the benefit of exchanging Stikeez with your friends (assuming you have any crazy enough to collect them).

Or buy it on Gumtree.

All graphs in this post were produced by this Jupyter Notebook. Feel free to download it, modify it and play with the data and methods yourself!